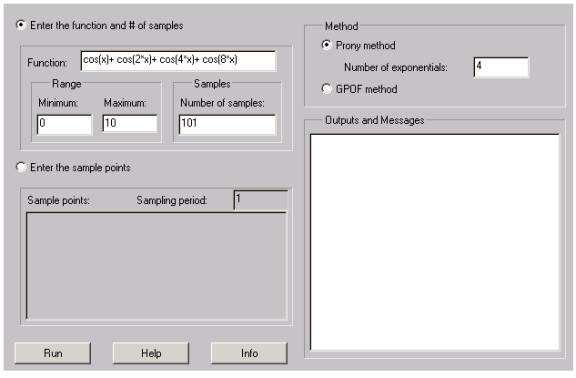
To run the program properly you must select options and enter inputs as follows:

• If you would like to run GPOF or Prony method on the samples gained from any function you choose “Enter the function and # of samples ” option. It is also selected by default. Next you should enter the function on the “Function” field. The format of the function you want to run should be as follows:

Function	Description
E	decimal exponent. For example, 2E3 is equal to 2000.
ln(x)	natural logarithm of x
Log(x)	decimal logarith of x
Exp(x)	e to the power of x
sqrt(x)	square root of x
Sin(x)	sine of x. NOTE: x is in radians not in degrees. To convert degrees to radians look at rad function
Cos(x)	cosine of x. NOTE: x is in radians not in degrees.
Tan(x)	tangent of x. NOTE: x is in radians not in degrees.
Cot(x)	cotangent of x. NOTE: x is in radians not in degrees.
asin(x)	inverse sign of x
acos(x)	inverse cosine of x
atan(x)	inverse tangent of x
pow(x,y)	x to the power y
sinh(x)	hyperbolic sine of x
cosh(x)	hyperbolic cosine of x
tanh(x)	hyperbolic tangentof x
coth(x)	hyperbolic cotangent of x
Abs(x)	absolute value of x
Rnd(x)	round x to the nearest integer value
Int(x)	integer part of x
Avg(x,y)	average value of x and y
Ran(x)	produces a random value between 0 and x (NOTE: if x is complex, then the produced number is also complex!)
Deg(x)	converts x to degrees (x is in radians) (NOTE: Only real parts of the numbers are used in calculations!)
Rad(x)	converts x to radians (x is in degrees) (NOTE: Only real parts of the numbers are used in calculations!)
Fact(x)	factoriel of x (NOTE: Only real parts of the numbers are used in calculations!)
Sgn(x)	sign of x (NOTE: Only real parts of the numbers are used in calculations!)
mod(x,y)	reaminder of x divided by y (NOTE: Only real parts of the numbers are used in calculations!)
Min(x,y)	minimum of x and y (NOTE: Only real parts of the numbers are used in calculations!)
Max(x,y)	maximum of x and y (NOTE: Only real parts of the numbers are used in calculations!)
cmplx(x,y) and cart(x,y)	creates a complex number, whose real part is x and imaginary part is y
mag(x)	magnitude of x
norm(x)	norm of x
Re(x)	real part of x
Im(x)	imaginary part of x
polar(x,y)	creates a complex number from polar coordinate (x,y)
conj(x)	complex conjugate of x
Sum(func, var, min, max)	does the arithmetic summation. func represents the function. var must be one of the variables x,y,z,t,u, or v. min is the firstvalue of var and max is the last value of var. For example, sum(x^2+1,x,1,10) adds all values of x^2+1 from x=1 to x=10. You can also do nested summations. For example to implement , you just need to write sum( z^2 + 2*sum(y^3*z ,y,-100,100), z, 1,100). (NOTE: Only real parts of the numbers are used in calculations!)
Mul(func, var, min, max)	This function is similar to sum function. The difference is that this function does multiplication instead of summation. (NOTE: Only real parts of the numbers are used in calculations!)

In this version, six variables are defined: x, y, z, t, u and v.
You can use ^ operator instead of pow(x,y).
Other operators are + - * / ( ) and . Moreover, PI is defined.

After the function is defined properly, what is next is to enter the sampling range. You enter the minimum point of this range in the “Minimum” field and the maximum point of the range in the “Maximum” field. You should also enter the number of samples in this range desired.

• If you want to enter the samples by hand, you just select “Enter sample points” option and in the “Samples” field you enter your samples one sample at each line. That is after one sample is entered, you should press enter and the procedure goes on like this until you have entered all of your sample points. Finished this part, next you enter the sampling period in the “Sampling Period” field.

• After specifying samples phase is completed, now you have to decide whether to use GPOF of Prony Method. İf you would like to use prony method then you should select “Prony Method” option and then you enter number of exponentials you want to fit to your data in the “No of Exponentials” field. If you would like to use GPOF, you just select “GPOF” option and number of exponentials that would be fit to your data is computed by the software itself. The underlying algorithm can be found in the Info section.

• After all these phases are successfully completed, you just click “RUN” button and outputs appear in the output field. “HELP” opens this page and “INFO” button opens a page in which you can find all the theoretical background and algorithms used in this program in addition to the sample runs of the software.

Software Developed by Fatih Unlu. Please feel free to send your questions and comments to funlu@princeton.edu.

I would like to send my special thanks to my supervisor Prof. M.I.Aksun (irsadi@ee.bilkent.edu.tr).