The Modified
Regula Falsi Method
1. Information
About the Modified Regula Falsi Method
Modified
Regula Falsi Method generates the approximations in the same manner as the
Regula Falsi Method does. But for faster convergence some modifications are
made. We first choose the initial approximations 
and 
with 
. The approximation 
is chosen as the
x-intercept of the line joining 
and 
. To decide which secant line to use to compute 
, we check 
. If this value is negative, then 
and 
bracket a root and we
choose 
as the x-intercept of
the line joining 
and 
. If not, we choose 
as the x-intercept of
the line joining 
and 
and then interchange the indices on 
and 
. In a similar manner, the following 
’s are calculated. This relabeling ensures that the root is
bracketed between successive iterations.
The
above explanation is described in the following algorithm. Figure.1 shows how
this algorithm is implemented.
Figure.1:
Modified Regula Falsi Method
INPUT:
endpoints 
, 
; tolerance TOL; maximum number of iterations N0
OUTPUT:
approximate solution 
or message of
failure.
Step 1: Set i =
2;
;
.
Step 2: While 
do steps 3-7
Step 3: Set 
(Compute pi.)
Step 4: If 
then
OUTPUT (p); (Procedure
completed successfully.)
STOP
Step 5: Set i = i+1;
Step 6: If 
then set 
;
.
Step 7: Set 
;
.
Step 8: OUTPUT
(Method failed)
(Procedure completed
unsuccessfully.)
STOP.
The
following procedures can be used as stopping criteria for the above algorithm.
In our program we use one of them or the both according the desire of the user.
The typical values for these criteria are set at the initial state of the
applet.
Absolute Error: 
Relative Error: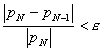 
2. Some Numerical
Results
f(x) = x3+4x2-10
The results of the
problem f(x) = x3+4x2-10 = 0 is obtained by using the
Modified Regula Falsi Method. The iteration number and the p value
obtained after this iteration are provided as follows:
IterationNumber |
Pn |
|
1 |
1.263157894736842 |
|
2 |
1.400403369320204 |
|
3 |
1.342145133684757 |
|
4 |
1.3748035389123485 |
|
5 |
1.3598670255622798 |
|
6 |
1.367732025551732 |
|
7 |
1.3639281150229308 |
|
8 |
1.3658662133784305 |
|
9 |
1.3649078080249408 |
|
10 |
1.365389970606483 |
|
11 |
1.3651497209704881 |
|
12 |
1.3652700739462054 |
|
13 |
1.3652099599732015 |
|
14 |
1.3652400338945831 |
|
15 |
1.3652001035925876 |
Table.1:
The results for the Modified Regula Falsi Method.
While
the above results are being obtained, the absolute error is chosen and its
value is 0.0001. The initial interval is [1,2]. The correct value of the root
is 1.365230013 (up to nine digits). The approximated value of root by this
method is 1.365200103. Then the absolute error is 0.00003 that is already
smaller than the desired value 0.0001.
f(x)=cos(x)-x
The results of the
problem f(x) = cos(x)-x = 0 is obtained by using the Modified Regula Falsi
Method. The initial interval is chosen as [0,1]. The iteration number and the p
value obtained after each iteration are provided as follows:
IterationNumber |
Pn |
|
1 |
0.6850733573260451 |
|
2 |
0.7731914418788256 |
|
3 |
0.7235874993260181 |
|
4 |
0.7470698118498033 |
|
5 |
0.7351221175987429 |
|
6 |
0.7410660783535018 |
|
7 |
0.7380925680968499 |
|
8 |
0.7395804042079531 |
|
9 |
0.7388371228632933 |
|
10 |
0.7392090141125577 |
|
11 |
0.7390231540774963 |
|
12 |
0.739116111201908 |
|
13 |
0.7390696408498045 |
Table.2: The
results for Modified Regula Falsi Method
The
absolute value of the error is again smaller than the desired value 0.0001.
That is the input for the applet by the user.
f(x)=ex^3–8
Because
of the shape (see the below figure) of the function in the interval [0,3] the
Regula Falsi Method couldn’t converge to a root after 100 iterations. The
iterations cannot leave the area where the change in the function is nearly
zero. If we use the Modified Regula Falsi instead of the Regula Falsi Method,
we obtain the following results.
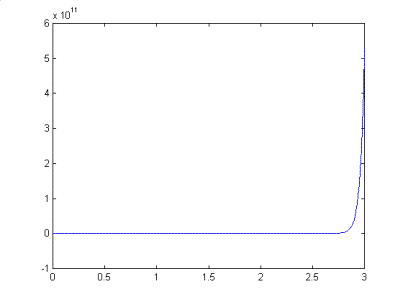
Figure.2: f(x)=ex^3–8
IterationNumber |
Pn |
|
1 |
3.9470105147395006E-11 |
|
2 |
1.1841031544010784E-10 |
|
3 |
2.7629073601722474E-10 |
|
4 |
5.920515771382235E-10 |
|
5 |
1.2235732592472813E-9 |
|
6 |
2.4866166229336375E-9 |
|
7 |
5.0127033481793115E-9 |
|
8 |
1.0064876790162508E-8 |
|
9 |
2.0169223640096295E-8 |
|
10 |
4.037791720383343E-8 |
|
11 |
8.079530378678597E-8 |
|
12 |
1.6163007477460422E-7 |
|
13 |
3.2329960803789376E-7 |
|
14 |
6.466386397150889E-7 |
|
15 |
1.293316563671973E-6 |
|
16 |
2.5866718539959587E-6 |
|
17 |
5.173380204286721E-6 |
|
18 |
1.0346787983454791E-5 |
|
19 |
2.06935678562602E-5 |
|
20 |
4.138698486073267E-5 |
|
21 |
8.27732479130008E-5 |
|
22 |
1.6554349025383808E-4 |
|
23 |
3.3107484038472003E-4 |
|
24 |
6.621010064743331E-4 |
|
25 |
0.001324007234196999 |
|
26 |
0.002647235529414968 |
|
27 |
0.005291357535624367 |
|
28 |
0.010570279599228245 |
|
29 |
0.02109096600130855 |
|
30 |
0.041984732269401234 |
|
31 |
0.08318978545001166 |
|
32 |
0.16332990643429346 |
|
33 |
0.3149604128619411 |
|
34 |
0.5864873603688315 |
|
35 |
1.0197841634381308 |
|
36 |
1.5112716280638492 |
|
37 |
1.0679008766032143 |
|
38 |
1.1928316349827386 |
|
39 |
1.2888335127317911 |
|
40 |
1.261458821312048 |
|
41 |
1.2802687918986537 |
|
42 |
1.2735758220744937 |
|
43 |
1.2774997520293316 |
|
44 |
1.2757532048019795 |
|
45 |
1.2766804084396108 |
|
46 |
1.27623350381156 |
|
47 |
1.2764614149990965 |
|
48 |
1.27634873039798 |
|
49 |
1.2764054163368483 |
|
50 |
1.2763771677821358 |
Table.3: The
results for Modified Regula Falsi Method
f(x)=xtan(x)-3
The
results of the problem f(x)=xtan(x)-3=0 is obtained by using the Modified
Regula Falsi Method. The initial interval is chosen as [6,7]. The iteration
number and the p value obtained after each iteration are provided as
follows:
IterationNumber |
Pn |
|
1 |
6.604885608786283 |
|
2 |
6.739248971974184 |
|
3 |
6.680962636531199 |
|
4 |
6.713462763424663 |
|
5 |
6.698605387698973 |
|
6 |
6.706441745550199 |
|
7 |
6.702658570642793 |
|
8 |
6.704588510644558 |
|
9 |
6.703634964556151 |
|
10 |
6.704114934190539 |
|
11 |
6.703875853443404 |
|
12 |
6.703995642904286 |
|
13 |
6.7039358167077685 |
|
14 |
6.703965748429587 |
Table.4:
The results for the Modified Regula Falsi Method
The
absolute value of the error is again smaller than the desired value 0.0001.
3. Conclusion
When the above examples
are examined it can be seen that the Modified Regula Falsi is faster than
Regula Falsi for some examples while there is no or less difference between the
iteration numbers for some others. The reason for this is the behavior of the
function in the given interval. The effect of the shape of the function on the
iteration number is explained in the above section. Then while deciding which
method to use, the user should know the behavior of the function in the desired
interval.
4. References
[1]
Numerical Analysis, R.L. Burden, J.D. Faires, PWS Publishing Company,
Boston 1993.