MBX Model For Micro Cells

This analytical model explicates the path loss as a result of signal reduction due to free space wave front spreading, multiple diffraction past rows of buildings, and building shadowing [1]. Model has been proposed for base station antennas near and below the average height of buildings surrounding the base station.

a) Path Loss Formula For Base Station Antennas Near The Average Rooftop Buildings

In this section, formula is derived by doing approximation as taking Dh_b=0 in equation in MBX model for macro cells.

(1)

Then, reduced field strength could be written as

(2)

By including free space loss and diffraction loss from rooftop to street following formula is proposed:

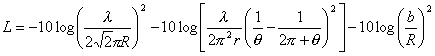
, in meters

Where,

q=tan^-1(Dh_m/x) in radians

d: average separation distance between the rows of buildings , in meters

R: mobile to base station distance in km.

In the equation above, a factor of two is included in free space loss term to account for the local scattering from obstacles surrounding the base station since base station is inside the clutter of buildings.

For a typical urban and suburban area terrain type, by using formula 2, it is found that path loss has 1/R⁴ distance dependence and 1/f³ frequency dependence.

a) Path Loss Formula For Base Station Antennas Below The Average Rooftop Buildings

(3)

For base station antennas below the average rooftop buildings, plane wave multiple diffraction is separated in two simpler cylindrical wave processes. The former, the cylindrical wave excited by a line source below the average roof top level is diffracted by the first row of buildings. The latter is given by Xia and Bertoni [2]. The field reduction combined for the two cases above yields following formula:

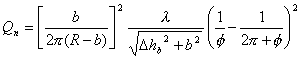
where, j=-tan^-1(Dh_b/b) in radians denotes incident angle to the first rows of the buildings. By accounting the free space and diffraction loss from rooftop to the street following formula is proposed for base station antennas below rooftop level.

(4)

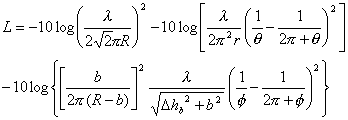
For typical urban and suburban environments, formula above yields 1/R⁴ distance and 1/f⁴ frequency dependence.

In [1], there are no restrictions for the maximum and minimum distances and applicable frequencies. This model is compared with the measurements conducted in some cities and countries, and comparison yields accurate correlation with model and measurements. Since all comparisons are done in 900 MHz and 1800 MHz band, this means model gives accurate results for frequency range 800<f <2000 MHz.

[1] Howard H.Xia, “A simplified Analytical Model for Predicting Path Loss in Urban and Suburban Environments”, IEEE Trans. Veh. Technol. Vol VT-46,No.4, 1997.

[2] W.C.Y.Lee, “ Mobile Cellular Telecommunications Systems”, New York,McGraw-Hill, 1989