Flat Edge Model

This model proposes a solution to propagation concept in built up areas by assuming all of the buildings to of equal height and spacing [1,2,3]. The values used can be average values for the area under consideration or could be calculated separately when urbanization varies significantly. The geometry for the model is shown in figure 1. In this figure the value of w should be effective one to account for the longer paths between the buildings for oblique incidence.

The total path loss is defined as

(1)

L = L_n(t)+ L_FS+ L_E

Where L_E represents single edge diffraction over the final building and L_n represents multiple diffraction over the remaining (n-1) buildings and L_FS is free space loss.

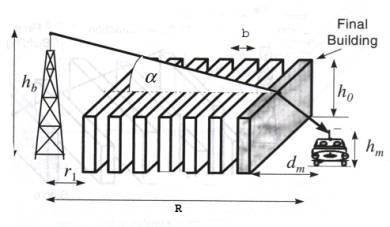
Figure 1 [1]. Geometry of Flat Edge Model

(2)

L_n is a function of parameter t, which is given by

where a is in radians, b and l are in meters.

For n ³ 1 (3)

Solution for L_n(t) is the following formula :

(4)

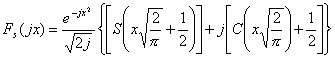
where L₀(t)=1 and

L_n(t) can be calculated from above equations or it may be calculated by following approximate formula

(5)

where c₁=3.29, c₂=9.9, c₃=0.77, c₄=0.26. For 1£ n£100 and -1£t<0.

This approximate formula deviates ± 1.5 dB from 3 for ranges of n and t given above.

(6)

Final building diffraction loss is obtained by following formula used in Ikegami model [4].

Where j is the angle between the street and the direct line from base to mobile and L_r=0.25 is the reflection loss.

In the model, it is observed that for large number of buildings, the model shows approximately same path loss exponent with measurements. Change of path loss exponent with respect to number of buildings is given in figure 2.

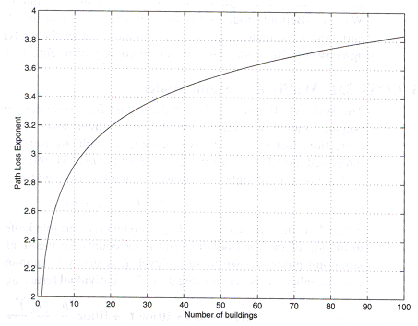
Figure 2 [1] Path Loss Exponent for the Flat Edge Model.

For small a value, and large number of buildings, multiple building diffraction loss is kept up with measurements, which have approximately 4 for path loss exponent. This is also shown by the following study done by using Wireless Simulator Program.

Terrain Parameters:

Average Width: 73.8 m

Average Building Height: 16m

Percentage of Buildings: 37%

Study Parameters:

Frequency: 900 MHz,

TX Height (hb)=31m

Mobile Height (hm)=1.5m

TX Gain: 13 dBi

City Size: Small/Medium

Area Type:

Modified Hata Path Loss :Open Area

Modified Hata Path Loss (1): Suburban Area

Modified Hata Path Loss (2): Urban Area

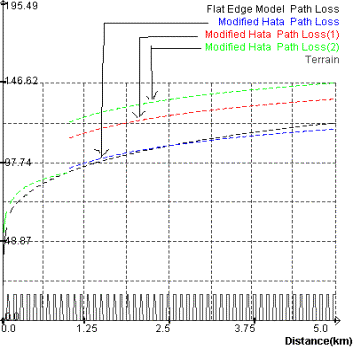
Figure 3 Comparison of Flat Edge Model with Modified Hata Model

As seen from the figure 3, as number of buildings is increased flat edge model correlates very much with Modified Hata model for the case when area type is open area. For the other area types suburban and urban area, two models are uncorrelated. Thereby, this result is valid for the equal heights of buildings.

Study Parameters:

Frequency: 900 MHz,

TX Height (hb)=51m

Mobile Height (hm)=1.5m

TX Gain: 13 dBi

City Size: Small/Medium

Area Type :

Modified Hata Path Loss :Open Area

Terrain Parameters:

Average Width: 73.8 m

Average Building Height: 16m

Percentage of Buildings: 37%

In order to show that flat edge model correlates with measurements when a is small, following study is done by using Wireless Simulator Program. In this study, transmitter height is taken to be 51 m to have small grazing angle a at far distance.

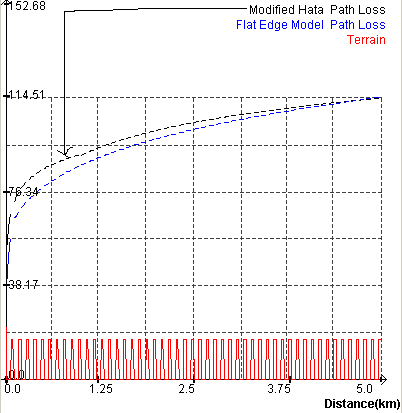
Figure 4 Effects of grazing angle for path loss exponent

In figure 3, flat edge model and Modified Hata model starts to correlate very well at distance about 2.5 km when Transmitter height is 31 m. For the figure 4, highly correlation between two models starts to occur at distance about 5km. These two studies prove that flat edge model starts to behave as measurements for small grazing angle values.

Study shown in figure 5 is done to show how flat edge model behaves for non-uniform building heights. Study implies that for non-uniform building heights, flat edge model doesn’t correlate with measurements even at higher number of buildings and smaller grazing angles. This is resulted from diffraction loss approach proposed by the model. Also, behavior of the model for non-uniform building heights is not ordinary. As mobile gets further distance from the transmitter, it is expected to have higher path loss. However, behavior of the model doesn’t keep up with real time.

Terrain Parameters:

Average Width: 73.8 m

Average Building Height: 16m

Percentage of Buildings: 37%

Study Parameters:

Frequency: 900 MHz,

TX Height (hb)=51m

Mobile Height (hm)=1.5m

TX Gain: 13 dBi

City Size: Small/Medium

Area Type :

Modified Hata Path Loss :Open Area

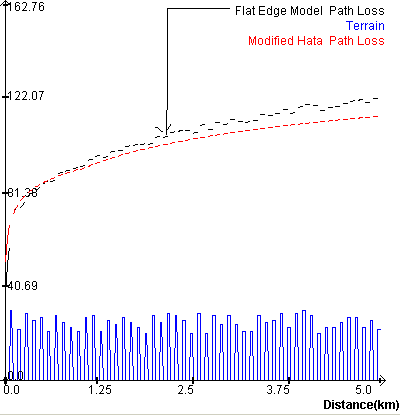
Figure 5 Comparison of two models for non-uniform building heights

Lots of comparison of Flat Edge model with measurements and other models are given in the literature. Following figures are a few of them. In figure 6 and 7, comparison of Flat Edge model with measurements and Hata urban models are given.

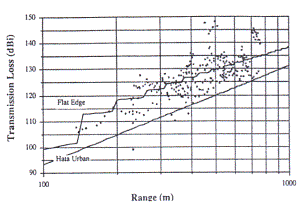
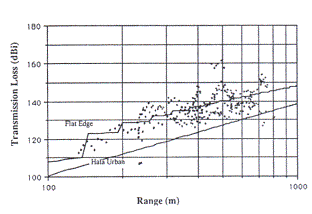
Figure 6 [3] Comparison of Flat Edge Model Figure 7[3] Comparison of Flat Edge Model

with measurements and Hata Urban Model with measurements and Hata Urban Model

at 1845 MHz at 955 MHz.

At 1845 MHz, flat edge model have a mean error of –0.6 dB and rms error of 6.1 dB and corresponding figure for Hata Urban model at the same frequency has a mean error of 12.5 dB and 6.1 dB. For the frequency 955MHz, -0.6dB and 5.6 dB for flat edge, respectively 9.7 dB and 5.5 dB for the Flat Edge model.

All these results summarize that if mean width and mean buildings heights are available Flat Edge Model makes an appropriate prediction.

For the irregular spacing and building heights, Vogler [5,6] proposed a fairly accurate solution to the problem, by calculating diffraction loss at each building edge, which requires multiple integral whose dimension is equal to number of buildings. Detailed explanation of Vogler method is given in appendix II. Since Vogler method is not efficient computationally, some methods, which approximate the problem by skipping a few of the edges, are recommended. One of these methods is proposed by Saunders [3] whose method, called hybrid method, rely on following algorithm:

• The first step is to ignore the any edges which are considerably lower than their neighbors therefore, since they don’t affect the result very much. This could be done by b_m parameter defined in Vogler method. For instance, for edges with less than some threshold b_m value are neglected. Overall characteristics of the profile are calculated by flat edge model and a linear regression through the edges are applied to find the effective grazing angle a and the mean building spacing w. Let’s call resulting electric field of this part call as E₁.

• Second step is to calculate the deviations from above case by using diffraction integral applied to most significant edges only. The number of edges used in integral will depend on application since there is trade-off between the number of edges used and the prediction accuracy. For instance, if 10 edges are considered as more significant, then 10 edges have most important b_m parameters are found as follow:
• Find the edge with most negative b_m value and remove this edge
• Recalculate the remaining parameters for remaining edges
• If more then 10 edges remained, redo two steps above.

The resulting field strength is found by using method given IIIB in[3] and call this as E₂.

• The third step is to calculate the field strength for 10 edges by using flat edge model with parameters found in first step and resulting electric field called as E_3.

Then, the overall field strength is found as

E₃=E₁E₂/E₃.

A comparison of this method with measurements is given in the following figure 8.

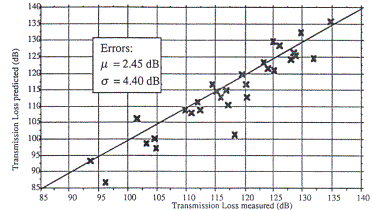
Figure 8 [3] Comparison of hybrid method with measurements at 933 MHz

[1] Sounders, Simon.R., “ Antennas and Propagation for Wireless Communication Systems”,Wiley,New York,1999

[2] Saunders, S.R., and Bonar, F.R., “ Explicit multiple-building diffraction attenuation function for mobile radio wave propagation”, Electron.Letts., Vol.27, No.14,1991, pp.1276-1277

[3] Saunders, S.R., and Bonar, F.R., “ Prediction of Mobile Radio Wave Propagation over Buildings of Irregular Heights and Spacings”, IEEE Trans. Antennas Propagat, Vol.42,No.2,1994,pp.137-143

[4] F.Ikegami, T.Takeuchi, and S.Yoshida, “Theoretical prediction of mean field strength for Urban Mobile Radio”, IEEE Trans. Antennas Propagat., Vol.39, No.3, 1991

[5] L.E. Vogler, “ The attenuation of Electromagnetic waves by multiple knife-edge diffraction”,NTIA Rep., Natl.Telecommun. and Inf. Admin, Boulder,Colo,1981.

[6] L.E. Vogler, “ An attenuation function for multiple knife-edge diffraction”, Radio Science,Vol.17,No.6,1982,pp.1541-1546